Aljabar Boolean

Aljabar Boolean

Oleh: Mohammad Rochfasingga

          3.34.15.0.14 | IK-1A | POLINES

            Aljabar Boolean adalah aljabar logika. Sifat biner proposisi / dalil logis (TRUE or FALSE) atau menggunakan  angka  biner  1  dan  0 menunjukkan mempunyai aplikasi dalam komputasi. Pelopornya George Boole. Ajaran boolean ini adalah memuat aturan umum dimana yang menyatakan hubungan antara input-input suatu rangkaian logika dengan output-outputnya. Aljabar Boolean digunakan untuk menganalisa dan menyederhanakan sirkuit  logika digital.

Berikut ini aturan penting yang digunakan pada Aljabar Boolean:

1. Variabel  yang  digunakan  hanya memiliki  dua  nilai.  Biner  1  untuk ON/HIGH  dan  biner  untuk OFF/LOW.
2. Komplemen dari suatu variabel diwakili oleh sebuah Strip atas (-). Dimana komplemen dari variabel Y diwakili , jika Y'=1 maka Y=0 dan jika Y=1 maka Y'=0.
3. Variabel OR diwakili oleh tanda plus (+) diantara variabel. Contoh variabel O X,Y,Z diwakili X+Y+Z.
4. Logika AND pada variabel dua atau lebih diwakili dengan menuliskan titik diantara variable seperti X.Y.Z. terkadang tidak diberi titik, hanya XYZ.

Aturan Persamaan Aljabar Boolean:

    Dari tabel aturan persamaan aljabar boolean diatas, mari kita buktikan sudah benarkah aturan tersebut. Sebagai buktinya kita akan membuktikan aturan Distributive berikut ini:

Aturan Distributive

X.(Y+Z) = (X.Y) + (X.Z)

1. Gerbang Logika

          X.(Y+Z) : 

(X.Y) + (X.Z) :

2. Tabel Kebenaran

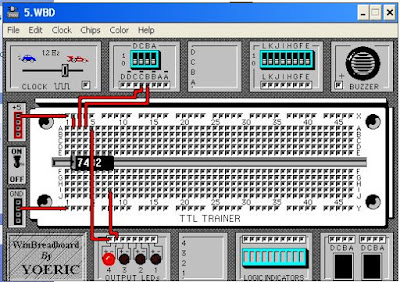
3. Pembuktian dengan WinBreadBoard

Dari pembuktian diatas, disimpulkan bahwa aturan tersebut benar.

Menyederhanakan suatu persamaan:

Jawab:

a)      

1.      Gerbang Logika 

2.      Tabel Kebenaran

3.      Rangkaian logika dengan WinBreadBoard

Penyederhanaan persamaaan dengan aturan aljabar Boolean:

1.      Penyederhanaan

2.      Gerbang Logika

3.      Tabel Kebenaran

4.      Rangkaian logika dengan WinBreadBoard

b)     

1.      Gerbang Logika

2.      Tabel Kebenaran

3.      Rangkaian logika dengan WinBreadBoard

Penyederhanaan persamaaan dengan aturan aljabar Boolean:

1.      Penyederhanaan

2.      Rangkaian Logika

3.      Tabel Kebenaran

4.      Rangkaian Logika dengan WinBreadBoard

Demikian penjelasan mengenai Aljabar Boolean, semoga berguna dan bermanfaat bagi kita semua. Terima Kasih!!!

Sumber Artikel :

            Rangkaian Logika Dasar Pertemuan 4 dan 5 - Aljabar Boolean dan Rangkaian Gerbang Logika - Copy.pdf

            http://slametwinardi.dosen.narotama.ac.id/files/2013/09/Aljabar-Boolean-pde.pdf