Aljabar Boolean
Sejarah Singkat
Diciptakan tahun 1854 dan diterbitkan pada bukunya “An Investigation of the Laws of Thought”.
Manfaat
- Aljabar Boolean digunakan untuk menangani persoalan-persoalan logika.
- Penerapan paling penting dalam aljabar boolean adalah penyederhanaan rangkaian logika.
Definisi Aljabar Boolean
- suatu himpunan B
- dua operator biner yang didefinisikan pada himpunan tersebut, yaitu :
– Penambahan (+)
Postulat Hutingtoon
- Closure :
- a + b Î B
- a . b Î B
- Identitas :
- Ada elemen unik 0 Î B, sehingga berlaku :
a + 0 = 0 + a = a
- Ada elemen unik 1 Î B, sehingga berlaku :
a . 1 = 1 . a = a
3. Komutatif :
- a + b = b + a
- a . b = b . a
4. Distributif :
- a . ( b + c) = (a . b) + (a . c)
- a + (b . c) = (a + b) . (a + c)
- (a . b) + c = (a + c) . (b + c)
5. Komplemen :
Untuk setiap a Î B, ada elemen unik a’ Î B, sehingga berlaku :
6. Terdapat paling sedikit dua buah elemen , a dan b Î B sedemikian sehingga a≠b.
TURUNAN POSTULAT HUTINGTOON
- Idempoten :
- a . a = a
- a + a = a
- Asosiatif :
- a + (b + c) = (a + b) + c
- a . (b . c) = (a . b) . c
diturunkan dari aksioma yang lain.
Perbedaan aljabar boolean dengan aljabar biasa
- Aksioma distributif a + (b . c) = (a + b) . (a + c) benar untuk aljabar boolean tetapi tidak benar untuk aljabar biasa,
- Aljabar boolean tidak memiliki kebalikan perkalian dan penjumlahan, oleh karena itu tidak ada opersi pembagian dan pengurangan,
- Aksioma ke-5 mendefinisikan operator komplemen yang tidak ada pada aljabar biasa,
- Aljabar biasa memperlakukan bilangan real dengan himpunan elemen yang tidak berhingga, aljabar boolean memperlakukan himpunan elemen B yang sampai sekarang belum didefinisikan.
Persyarat aljabar boolean
- Menentukan elemen himpunan B,
- Menentukan aturan operasi untuk operator biner,
- Himpunan B bersama-sama dengan aturan operator biner tersebut harus memenuhi Postulat Huntington.
Ulasan Singkat
Hukum Identitas
Hukum Involution
Hukum Commulative
Hukum Associative
Hukum Distributive
Hukum Absorption
Hukum ini terbentuk dari 2 operator, yaitu AND dan OR
A+B.C = (A+B).(A+C)
Pembuktian:
A + B.C = A.1 + B.C [ karena, A.1 = A]
= A.(1 + B) + B.C [karena, B+1 = 1]
= A.1 + AB + BC
= A.(1 + C) + AB + BC [karena, A.A = A.1 = A]
= A.(A + C) + B.(A+C)
A + B.C = (A+B).(A+C) (terbukti)
Gerbang Logika Distributive
TABEL KEBENARAN
Implementasi pada WInbreadboard
X.(Y+Z)=(X+Y).(X+Z)
X.(Y+Z)
input 000
input 001
input 010
input 100
input 100
(X+Y).(X+Z)
input 001
input 010
input 011
input 100
Penyelesaian Persamaan 1
SOAL
JAWAB
Gerbang Logika Persamaan 1
Tabel Kebenaran Persamaan 1
Penyederhanaan Persamaan 1
Tabel Kebenaran Setelah Persamaan 1 Disederhanakan
Gerbang Logika Persamaan 1 Setelah Disederhanakan
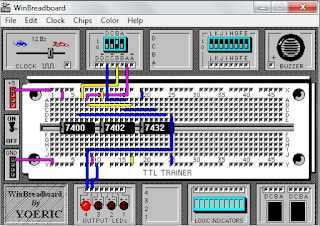
Winbreadboard
Sebelum disederhanakan
input 010
input 011
input 100
Setelah disederhanakan
input 001
Penyelesaian Persamaan 2
SOAL
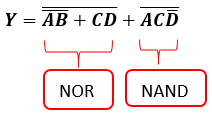
JAWAB
Gerbang Logika Persamaan 2 Sebelum Disederhanakan
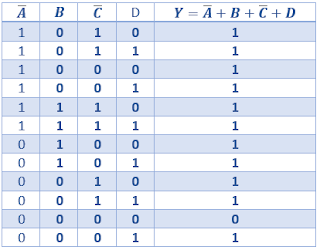
Tabel Kebenaran sebelum disederhanakan
Langkah penyederhanaan
Tabel Kebenaran setelah disederhanakan
Winbreadboard sebelum disederhanakan
input 0000
input 1111
Gerbang Logika Persamaan 2 Setelah Disederhanakan
Winbreadboard setelah disederhanakan
input 1000
input 0000
source:
http://dwiwisnumurti.blogspot.co.id/2012/04/hukum-hukum-dan-pembuktian-pada-aljabar.html
https://id.wikipedia.org/wiki/Aljabar_Boolean
- a + b Î B
- a . b Î B
- Ada elemen unik 0 Î B, sehingga berlaku :
- Ada elemen unik 1 Î B, sehingga berlaku :
- a + b = b + a
- a . b = b . a
4. Distributif :
- a . ( b + c) = (a . b) + (a . c)
- a + (b . c) = (a + b) . (a + c)
- (a . b) + c = (a + c) . (b + c)
5. Komplemen :
Untuk setiap a Î B, ada elemen unik a’ Î B, sehingga berlaku :
a + a’ = 1 dan a . a’ = 0
- a . a = a
- a + a = a
- a + (b + c) = (a + b) + c
- a . (b . c) = (a . b) . c
Ulasan Singkat
Hukum Identitas
Hukum identitas menunjukan bahwa gerbang X jika ditambah 0 sama dengan X dan jika X dikali 1 sama dengan X
Hukum Komplemen
Hukum Involution
Hukum involution menunjukkan jika gerbang yang sudah ada aksen(not) jika di not kan maka hasilnya sama dengan bilangan itu sendiri tanpa diberi aksen.
Hukum Commulative
Berdasarkan hukum kumulatif, urutan dari operasi OR dan AND pada suatu variabel tidak membuat perbedaan
Hukum Associative
Hukum ini memuat beberapa variabel, di mana operasi OR dari variabel hasil adalah sama meskipun pengelompokan variabel. Hukum ini mirip dengan kasus AND.
Hukum Distributive
Hukum De Morgan
Teorema lain yang digunakan dalam gerbang digital adalah teorema de Morgan. Teorema de Morgan dapat dinyatakan dalam persamaan sebagai berikut :
Hukum Absorption
Hukum ini terbentuk dari 2 operator, yaitu AND dan OR
Marilah kita lihat bagaimana pembuktian dari hukum distributive aljabar boolean...
A+B.C = (A+B).(A+C)
Pembuktian:
A + B.C = A.1 + B.C [ karena, A.1 = A]
= A.(1 + B) + B.C [karena, B+1 = 1]
= A.1 + AB + BC
= A.(1 + C) + AB + BC [karena, A.A = A.1 = A]
= A.(A + C) + B.(A+C)
A + B.C = (A+B).(A+C) (terbukti)
TABEL KEBENARAN
Implementasi pada WInbreadboard
X.(Y+Z)=(X+Y).(X+Z)
X.(Y+Z)
input 000
input 001
input 010
input 100
input 100













































No comments:
Post a Comment