Karnaugh Map (disingkat K-map) adalah
sebuah peralatan grafis yang digunakan untuk menyederhanakan persamaan logika
atau mengkonversikan sebuah Tabel Kebenaran menjadi sebuah rangkaian Logika.
Blok diagram sebuah K-map seperti gambar 5-1 di bawah ini. AB dan C adalah
variabel input, output-output berupa minterm-minterm bernilai 1 diisikan pada
sel K-map. Jumlah sel K-map adalah 2.
Langkah-langkah
dalam menggunakan K-map adalah sebagai berikut :
1. Konversikan persamaan
Boolean yang diketahui ke dalam bentuk persamaan SOPnya (Sum of Product).
Gunakan Tabel Kebenaran sebagai alat bantu.
2. Gambarlah K-map, dengan
jumlah sel = 2 jumlah variabel input.
3. Isi sel K-map sesuai dengan
minterm pada Tabel Kebenaran .
4. Cover minterm-minterm
bernilai 1 yang berdekatan, dengan aturan :
·
hanya minterm berdekatan secara vertikal atau horizontal yang
boleh di-cover.
·
Jumlah minterm berdekatan yang boleh di-cover adalah : 2. 4, 8,
16, 32
5.
Buat persamaan SOP baru sesuai dengan hasil peng-cover-an minterm.
Dari persamaan SOP yang didapatkan, bisa
digambarkan rangkaian hasil penyederhanaannya.
Contoh Soal :
A. PENJABARAN IDE
Sebuah
pabrik kimia memerlukan alarm untuk menandai terjadinya kondisi kritis pada
salah satu tankinya. Masing-masing tanki mempunyai 4 buah switch HIGH/LOW yang
memonitor :
- Temperatur (T)
- Level Fluida (L)
- Tekanan (P)
- Bobot (W)
Kondisi : High (1) Low (0)
Disain sistem yang bisa mengaktifkan alarm jika kondisi-kondisi di bawah ini terjadi:
- Level Fluida, Temperatur dan Tekanan adalah HIGH.
- Level Fluida LOW, Tekanan dan Bobot HIGH
- Level Fluida dan Temperatur LOW, Tekanan HIGH
- Level Fluida dan Bobot LOW, Temperatur HIGH.
B. MENENTUKAN INPUT/OUPUT
INPUT
- Temperatur (T)
- Level Fluida (L)
- Tekanan (P)
- Bobot (W)
OUTPUT
Alarm (X)
C. MENGIMPLEMENTASIKAN KE DALAM TABEL KEBENARAN
Tekanan(P) : High (1)
Low (0)
Level Fluida(L) : High (1)
Low (0)
Temperatur(T) : High (1)
Low (0)
Bobot(W) : High (1)
Low (0)
Alarm(X) : High (1)
Low (0)
Sehingga SOP nya adalah :
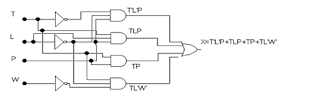
X = T’L’PW’ + T’L’PW + T’LPW + TL’PW’ + TLPW’ +TLPW
Maka Penyederhanaan SOP nya menjadi : X = TP + L'P +TL'W'
E. IMPLEMENTASI KE DALAM RANGKAIAN LOGIKA