Menyederhanakan Rangkaian Logika Dengan Metode K-Maps

K-Map berasal dari nama penemunya Maurice Karnaugh dan merupakan singkatan dari Karnaugh Map, salah satu cara alternatif untuk menyederhanakan rangkaian gerbang logika  selain  menggunakan  aljabar  Boolean,  dengan  menggunakan  K-Map  kita  dapat menyederhanakan  rangkaian  logika  yang  berasal  dari  tabel  kebenaran  dan  aljabar Boolean  SOP (Sum Of Product) / POS (Product Of Sum)  dengan  output  0  atau  1  yang dimasukkan ke dalam peta Karnaugh. K-Map lebih praktis untuk jumlah variabel yang kurang dari 6, dan dengan menggunakan K-Map dapat dihasilkan persamaan elementer (tidak dapat disederhanakan lagi).

Prosedur dalam pemakaian K-Maps adalah :

 a.  Konversikan persamaan Boolean yang diketahui ke dalam bentuk persamaan  SOP-nya (Sum of Product). Gunakan Tabel Kebenaran sebagai alat bantu.

b.  Gambarlah K-map, dengan jumlah sel = 2^{jumlah variabel input}

c.   Isi sel K-map sesuai dengan minterm pada Tabel Kebenaran

d.  Cover minterm-minterm bernilai 1 yang berdekatan, dengan aturan :

·  Hanya minterm berdekatan secara vertikal atau horizontal yang boleh di-cover.

·  Jumlah minterm berdekatan yang boleh di-cover adalah : 2. 4, 8, 16, 32

e.  Buat persamaan SOP baru sesuai dengan hasil peng-cover-an minterm.

Berikut adalah langkah merancang rangkaian logika : 

  1.  Penjabaran Ide

  2.  Menentukan jumlah variable input dan output yang dibutuhkan

  3.  Mengimplementasikan ide kedalam tabel kebenaran

  4.  Penyederhanaan fungsi boolean

  5.  Implementasi ke dalam rangkaian logika

Contoh Soal dan Pembahasan : 

Jawab : 

Langkah - langkah penyederhanaan :

A.  Penjabaran Ide

• Level Fluida, Temperatur dan Tekanan adalah HIGH. 
• Level Fluida LOW, Tekanan dan Bobot HIGH
• Level Fluida dan Temperatur LOW, Tekanan HIGH
• Level Fluida dan Bobot LOW, Temperatur HIGH.

B.  Menentukan jumlah variable input dan output yang dibutuhkan

• 4 Input

               1. Temperatur

               2. Level Fluida

               3. Tekanan

               4. Bobot

• 1 Output

               1. Alarm

C.  Mengimplementasikan ide ke dalam tabel kebenaran

D.  Penyederhanaan fungsi boolean

        Sehingga penyederhanaannya menjadi :

E.  Gambar rangkaian logika
   
     1. Implementasi rangkaian gerbang logika

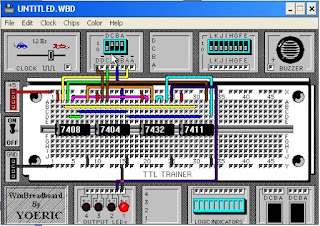
     2. Implementasi pada WinBreadBoard