Bener Gak Ya, Kalau X+(X.Y) = X? Yuk Kita Buktikan!

Sudah bukan rahasia lagi, kalau persamaan aljabar boolean bisa direpresentasikan ke dalam rangkaian logika. Jika dalam artikel ini sudah dijelaskan bagaimana cara menguji tabel kebenaran menggunakan aplikasi WinBreadBoard dan aplikasi online 123D Circuits, nah, di artikel berikut, kita akan membuktikan aturan-aturan boolean menggunakan aplikasi tersebut juga lho.
Sebelumnya, kamu tau gak aljabar boolean itu seperti apa? Aljabar Boolean itu, memuat aturan-aturan umum (postulat) yang menyatakan hubungan antara input-input suatu rangkaian logika dengan output-outputnya. Dalam aljabar boolean, terdapat aturan-aturan yang dinyatakan dalam sebuah persamaan Boolean. Berikut merupakan tabel aturan-aturan boolean:

Aturan-Aturan Boolean

Disini kita hanya akan membuktikan aturan Distributive, De Morgan, dan Absorption.

Distributive

- X.(Y+Z) = (X.Y)+(X.Z)
 Persamaan aljabar boolean diatas memiliki tabel kebenaran dan gambar rangkaian logika seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard

Schematic 

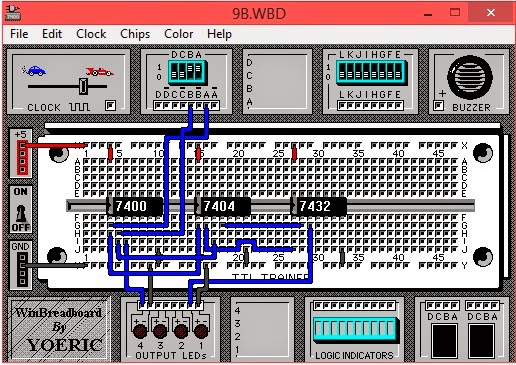
WinBreadBoard

- X+(Y.Z) = (X+Y).(X+Z)
 Persamaan aljabar boolean diatas mempunyai tabel kebenaran seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard
Schematic
WinBreadBoard

De Morgan

- ~(X+Y) = ~X.~Y

 Persamaan aljabar boolean diatas memiliki tabel kebenaran seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard
Schematic
WinBreadBoard

- ~(X.Y) = ~X+~Y
 Persamaan aljabar boolean diatas memiliki tabel kebenaran seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard
Schematic
WinBreadBoard

Absorption

- X+(X.Y) = X
Persamaan aljabar boolean diatas memiliki tabel kebenaran seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard
Schematic
WinBreadBoard

- X.(X+Y) = X
Persamaan aljabar boolean diatas memiliki tabel kebenaran seperti berikut:

Aturan diatas bisa dibuktikan menggunakan simulasi melalui 123D Circuits.

Breadboard
Schematic
WinBreadBoard

Nah, begitulah cara membuktikannya. Sekarang udah tau kan? Hehe. Semoga artikel ini bermanfaat ya. Happy learning! :)